Гидравлические
опоры
Гидравлические опоры
объединяют в себе упругий элемент и гидравлический гаситель колебаний. В
конструкции нет трущихся частей с фрикционным сухим контактом. Изменение объемов
полостей с жидкостью происходит за счет деформации эластичной обечайки гидравлической
опоры. В качестве компонентов трения выступают конструкционное трение и
гидравлическое вязкое сопротивление жидкости. Диссипация энергии колебаний в
гидравлических опорах происходит в реологической жидкости, заполняющей
внутренние полости конструкции, за счет совершения работы по перемещению
жидкости из одной камеры в другую полость. При этом выделяемая тепловая энергия
рассеивается в окружающую среду через металлические корпусные детали
гидравлической опоры. Обычно верхняя часть гидравлической опоры закрепляется на
двигателе, а основание на стационарной конструкции. Когда гидравлическая опора
нагружается от двигателя или от основания, объем верхней камеры изменяется и
вынуждает жидкость течь через отверстия в нижнюю камеру. Для повышения
эффективности виброизоляции предложены различные конструкции гидравлических
опор, которые обобщенно можно отнести к одному из нижеперечисленных четырех
типов гидравлических опор: с простым дроссельным отверстием; дроссельной
инерционной трубкой; дроссельной инерционной трубкой или отверстием с
разделительной мембраной; с введением активного управления, дополняющего
пассивные свойства.
Схема простейшей реальной гидравлической
опоры, предназначенной для демпфирования нежелательных колебаний средней
мощности, например, вибраций мотор-компрессора, представлена на рис. 1. Здесь 1
– поршневая полость, 2 – резиновая обечайка, 3 – опорная плата, 4 – корпус, 5 –
перегородка,6 – кольцо, 7 – мембрана, 8 – поддон, 9 – компенсационная полость,
10 – дроссельный канал, 11 – карман, 12а – дроссельный канал из поршневой
полости в карман, 12б – дроссельный канал из компенсационной полости в карман.
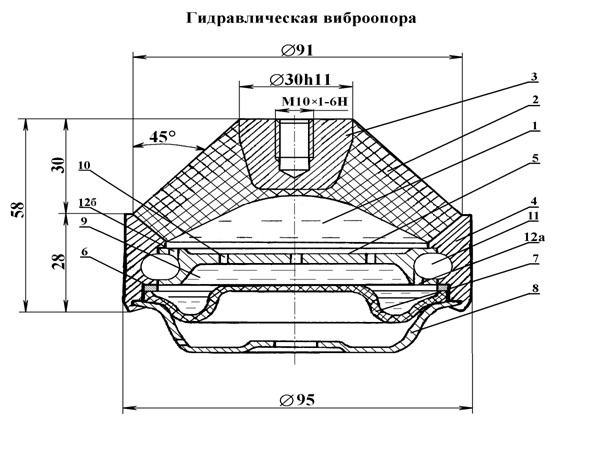
Рис. 1. Гидравлическая опора.
Динамическая
жесткость гидравлических опор
Динамической жесткостью
механической системы называют отношение амплитуды внешней гармонической силы к
комплексной амплитуде колебаний. Это понятие вводится по аналогии со
статической жесткостью, как отношение силы к смещению в системе, вызванному
данной силой. Для системы без демпфирования это действительная величина. Вблизи
резонанса система обладает минимальной динамической жесткостью. В частности,
для системы без демпфирования при резонансе динамическая жесткость равна нулю. Силы,
действующие на обечайку извне, вызывают деформацию обечайки и создают поток
жидкости в рабочей камере. Задача состоит в определении реакции системы на
внешнее воздействие в виде некоторой функции, зависящей в общем случае, как
минимум, от упругих деформаций, скорости деформаций и от температуры. Если предполагать
эту функцию гладкой, то первые члены ее разложения в ряд относительно
статического состояния будут моделировать соответствующую линеаризованную
подсистему исходной системы. Выражение для динамической жесткости линеаризованной
подсистемы в случае малых колебаний таково:
(1) 
,
где 
– приведенная масса;
– приведенный коэффициент демпфирования; 
– эквивалентная
жесткость, учитывающая взаимодействие мембраны и нижней камеры; 
– жесткость,
учитывающая сжимаемость жидкости в рабочей камере, 
– жесткость обечайки; 
– переменная преобразования Лапласа. Для сравнительной оценки
жесткостей примем объем рабочей камеры в виде объема усеченного конуса, с размерами,
показанными на рис. 20, равным 
, тогда 
. Пусть жесткость обечайки 
, а приведенная жесткость дополнительной камеры 
. Следовательно, жесткость жидкости на шесть порядков превышает
жесткость основного упругого элемента. Тогда можно принять упрощающее допущение
о несжимаемости жидкости в гидравлической опоре. Однако, с ростом деформаций
линеаризованная модель динамической жесткости (1) становится неадекватной физическому
процессу [1]. В этом случае эффективными способами решения проблемы являются детальные
расчеты методами МКЭ [2], применение генетических алгоритмов [3] и комплексные методы
модального анализа [4], сочетающие в себе наиболее выигрышные стороны
экспериментального и теоретического исследований.
[1] Farhad S. Samani, Francesco Pellicano. Vibration reduction of beams under successive traveling
loads by means of linear and nonlinear dynamic absorbers. Journal of Sound and
Vibration. Volume 331, Issue 10, 7 May 2012, Pages 2272–2290.
[2] H. P. Liu and T. X. Wu. Modelling and Performance Analysis of Rail
Vibration Absorber by FE and BE Methods. Noise and vibration mitigation for
rail transportation systems. Notes on Numerical Fluid Mechanics and
Multidisciplinary Design, 2012, Volume 118/2012, 135-142, DOI:
10.1007/978-4-431-53927-8_16
[3] Giorgio Bonori, Marco Barbieri, Francesco
Pellicano. Optimum profile modifications of
spur gears by means of genetic algorithms. Journal of Sound and Vibration. Volume 313, Issues 3-5, 17 June 2008,
Pages 603–616
[4] Barbara Tiseo, Antonio Concilio, Salvatore Ameduri, Antonio
Gianvito. A shape memory alloys based tuneable dynamic vibration absorber for
vibration tonal control. Journal of Theoretical and Applied Mechanics. 48, 1,
pp. 135-153, Warsaw 2010.